A short break to talk about location representation
27 Apr 2012I want to digress a bit from the Android specific portion of this project and talk a little bit about some of the library classes – or at least potential future library classes…
What I’d really like to talk about is how to represent Latitude and Longitude. This project is all about two extremes – small mobile devices and potentially HUGE sets of data. In both cases, it makes sense to use a nice small economical representation of your data. Comma separated ASCII text files may be convenient for human consumption, but they’re wasteful in terms of space, and humans won’t be the primary consumers or producers of these files, so that seems a silly option. What about some of the more computer readable options? Hmm, there’s always Integers. “But latitudes and longitudes are whole numbers!” you say. Fine, what do you suggest? Floating point numbers? In fact double precision floating point numbers seem to be the defacto standard that most libraries use to hand back latitude and longitude. That doesn’t mean it’s a good idea – I think the main reason they do it is because most of the libraries used to calculate the values are built on top of floating point math. That makes sense because floating point math (while being potentially slow and inefficient) is wonderfully generic and portable. Nobody wants to bother writing custom math libraries to handle various fixed point situations, but that doesn’t mean floating point makes sense for internal and external storage of the values!
“Why not?” you ask.
Because in this case we know there is a finite range that our values will always fall within – and that’s the exact opposite of what floating point numbers are intended for handling. Floating point numbers let you represent both REALLY HUGE and really small numbers, but we don’t need to handle latitudes like 56 bazillion or 0.00000000000000000000000000023. Note while the latter example is small, it doesn’t have many significant digits – it’s just 2.3*10^-28 (or something like that – it’s hard to count that many zeroes). There’s no reason we want to know latitude down to the nearest nanometer just because we’re near the equator or the same for longitude just because we’re near the prime meridian. We’d like a solution which provides even precision around the globe (let’s for a moment just ignore the fact that longitude itself has issues of warping as you get closer to the poles).
Microdegrees are one such option – with a circumference of a little over 40 thousand kilometers (or 40 million meters), 360 million distinct microdegree values pretty much means you pin point a single location to within about 10 centimeters (40m / 360 = .11m = 11cm). That seems more than sufficient for the purposes of this project, and it would be convenient because it seems to be the approach Google has taken for most of their mapping apis. There’s one problem – **I don’t like it**. Maybe it’s just me, but it seems like whoever came up with the approach was very much indoctrinated in thinking with decimal numbers and measuring in degrees. Both 10 and 360 are pretty arbitrary numbers – don’t get me wrong – they’re great for people who grew up learning mathematical algorithms and shortcuts specific to the decimal system, but we can move passed that – people won’t be crunching our numbers, computers will. And computers use **BINARY**!
So why not take advantage of this already? Here’s another arbitrary number – 32. It just so happens to be the number of bits that most of the phones we’ll be dealing with can currently process at a time. Java calls 32 bit signed fixed point numbers Integers. 32 bits means 4294967296 distinct values. That’s 11 times as many distinct values as you get from microdegrees. Am I saying I want to pin point locations down to one centimeter? NO! I’m just saying I don’t see any value in chosing an arbitrary number like 73 to base my entire system on. I want to pick a number that makes life easier for me. 360,000,000 only makes it easier for me to see with my eyes the similarity between 87.123456 degrees and 87123456 microdegrees. It doesn’t make it easier for my phone.
“But computers are faster at math than humans are!”
Ok, you got me there. Computers are supposed to make our lives easier, not the other way around. So now I’m going to argue that using binary values will make our lives as programmers easier rather than harder. You probably learned as a kid that it’s really easy to divide or multiply by 10 – you just add or remove a zero from the end of the number, or move the decimal place one way or the other. The only reason that works is because you’re dealing with decimal numbers – the trick is true for any base system when you’re multiplying or dividing by the value of the base. For binary that means multiplying or dividing by two. Why would you care about that? Well, if you’re doing it a lot, you can simply shift your bits to the right or left – just like shifting the decimal point.
Around the world in 80 days
Here’s another thing that’s nice about going with a binary approach. Think of the odometer in your car. What happens when it reaches it’s maximum value of 99999.9? The next thing it does is roll over to 00000.0! Now nobody actually believes that your dilapidated old jalopy just came off the showroom floor – but then again, wouldn’t it be nice if once you’re odometer started over at 0, your car was returned to it’s brand new show room look and feel? Or even if you at least could just get back that new car smell =)
Well it just so happens geography does work that way. When the odometer turns back over to 00000.0, the car goes back to its initial state – figuratively speaking. In this case what I’m really saying is that when you drive around the world at the equator (you’ve seen the bridge, right?) and you get to microdegree marker 359,999,999 and you go one microdegree past it to 0, you’ve actually returned to your starting point. Unfortunately, if you’re using microdegrees (and you don’t include any special logic to reset your odometer), your meter will keep right on going up to 360,000,001 and beyond. On the other hand, if you use a binary odometer, and you measure your longitude in binary degrees (I wish I new the official name for such a measurement), and you run out of digits on your odometer, you do actually cycle back to zero.
I could go on with this, but let’s just suffice it to say at this point that I see a number of advantages to using a true binary system for storing latitudes and longitudes. So rather than continuing to argue why, maybe I should just do my best to give a basic explanation of what it looks like and how you do it.
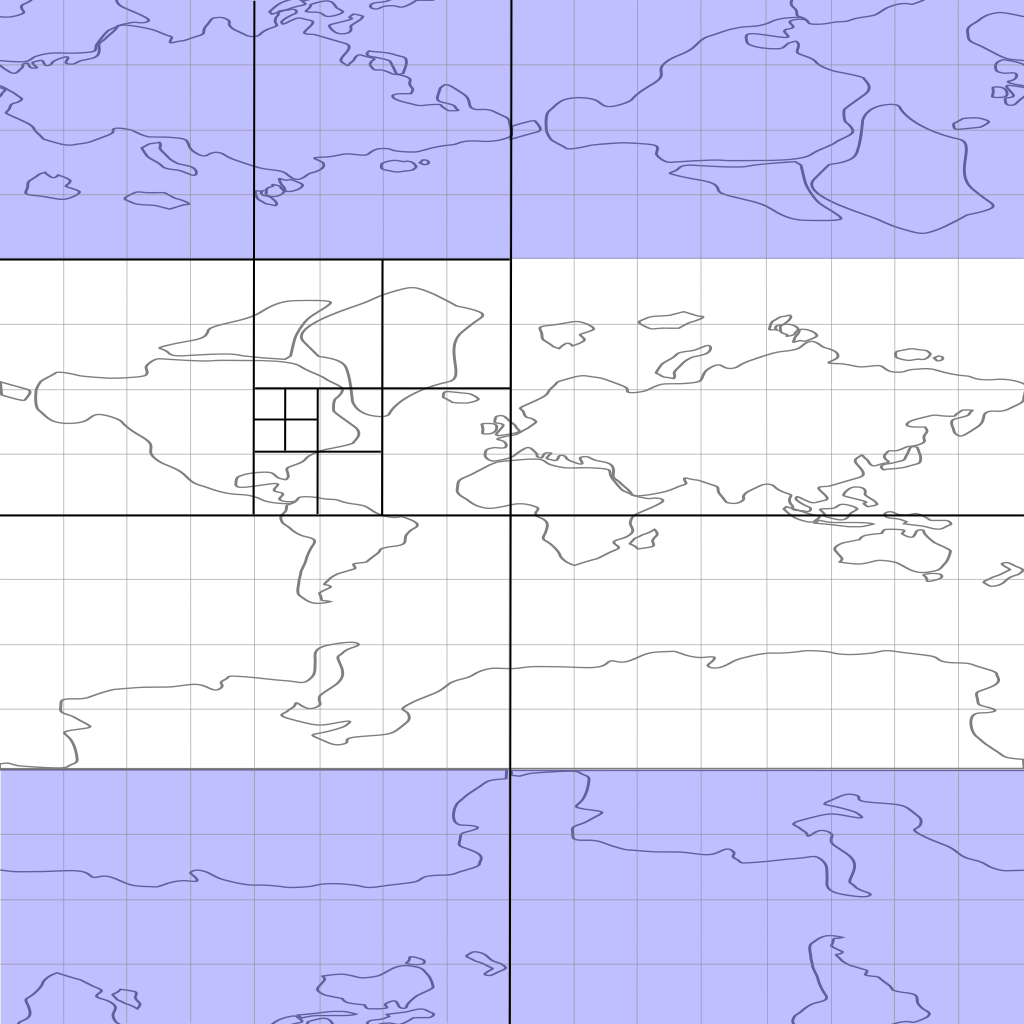
I’m no artist, but I’ve done my best to sketch up a rough map of the world and what it would look like in the representation I’m proposing. I don’t think this is really anything new – it’s pretty much the basis for geohash values proposed by Gustavo Niemeyer in 2008. While GeoHashing seems to be about representing the values in a base64 encoded value, I’m predominantly just interested in using an interleaved system of Morton numbers here to optimize the handling of the values. But there I go digressing again… If you look at my very rough sketch of the world, you’ll notice a few things – first of all, there are actually two copies! If you look at the greyed out portions in the top and bottom quarter of the sketch, you’ll see a second bizaro version of the world. This is actually fully consistent with a coordinate system of latitude and longitude where I’m showing both from negative 180 degrees to positive 180 degrees (top to bottom and left to right).
As you may already know, standard longitudes range from -180 to +180 where both -180 and +180 represent the same line of longitude, but latitude generally only ranges from -90 to +90. That doesn’t mean +181 isn’t a valid longitude or that +91 isn’t a valid latitude – it simply means that there are infinitely many ways to describe the same point on the globe. For clarity and sanity sake, we generally agree to refer to points unambiguously using a canonical form that limits the range of longitudes from -180 to 180 and latitudes from -90 to 90. Here’s the key point I want to make with this drawing – while longitude is cyclical like that odometer – once you get to 179.9999, it starts over at -180.0000, because of the canonical range we limit our latitudes to, it might at first glance seem that the same thing isn’t true. After all, when you get to the north pole, if you take another step you don’t suddenly find yourself at the south pole! However, what the greyed out portions of the map demonstrate is that while you don’t go directly from the north pole to the south pole, you can find yourself in a bizaro world in between.
Taking a walk on the Bizaro side
Suppose you happen to find yourself taking a stroll in Antarctica (it could happen!) and you started your hike at lat=-89.9999, long= 45.0000. From that point you decide to head straight south toward and inevitably right through the pole. Rather than turn around you decide to continue heading south in bizaro world.
“But that’s not possible!” you say.
In our world it may not be possible, but in bizaro world, things are a bit different. After all, in our world you can’t go any further south than the south pole. Once you pass it you’re heading north again. So normally you would pass start out at lat=-89.9999, long=45.0000 and eventually find yourself back at lat=89.9999 but long=-135.0000. However, in bizaro world you continue to move south to lat=90.0001 and the same long=45.0000 that you started on. What’s going on here? Bizaro world is just a mirror image of the real world. Rather having to change switch your longitude and bearing, we simply accept two redundant mirror images of the world into our mapping system. I’m not suggesting we introduce this bizaro world into our Canonical lat/long coordinate system, I’m just pointing it out for the pedagogical purpose of showing that longitude, just like latitude, is in fact cyclical – and just like longitude, it’s period is 360 degrees. So if you start somewhere at the equator and you circumnavigate the world, always traveling “South” (making half of your trip through bizaro world), eventually half way along your trip you will reach the equator at latitude -180 and you’re latitudinal odometer will roll all teh way over to +180 at which point you can continue south another 180 degrees to your starting point.
Try it. Draw any line and you’ll see if you go off the map on one edge, you can continue moving from the same location on the opposite edge. It’s fully consistent and, like I said, while I don’t suggest going around reporting locations and bearing in the bizaro side of the world, it’s definitely useful to recognize the implications of it’s existense on representational systems.
For one, it means that given such a system, you can safely and consitently perform any lateral transformation (up, down, right, left) of the full coordinate system and safely find yourself in a new valid coordinate system.
“Why would you want to do that?” you ask!
Ah, why that’s a wonderful segue! Thank you for asking!
GeoHashing and the edge problem
One of the problems people typically point out with using GeoHashes and interleaved Morton numbers in general is the edge problem. The main advantage to GeoHashes and Morton numbers is that locations which are nearby each other will tend to start with the same prefixes. For simplicity’s sake, lets go back to a simple one dimensional problem. Imagine a line that ranges from 0 to 1. Now picture three points on that line – 0.31, 0.37 and 0.51. If you wanted to know which point was closest to the 0.37, you’d have to subtract it from each of the other numbers and take the absolute value to get the distance. Clearly 0.31 is the closer of the two points. Suppose you were lazy and didn’t want to do all that math though, and maybe you have a lot more than just three numbers. Rather than calculating the distance between ever combination of numbers, you could simply create 10 buckets or ranges of numbers, then put each number into one of those ten buckets and limit your search for the nearest neighbor to those values in the same bucket. In this case, obvious buckets would be 0.00 - 0.09, 0.10 - 0.19, 0.20 - 0.29, etc. The easiest way to assign a number to it’s bucket would simply be to truncate everything after the first decimal place.
While this is fast and will work for finding approximate nearest neighbors, it has it’s problems. Edge conditions created by points like 0.39 and 0.40 for instance. While these two points are very close to one another, they would end up in separate buckets and never compared. One simple solution it to create two sets of buckets – one that truncates and one that rounds numbers to their nearest bucket. Then when looking for a points nearest neighbor, figure out the set of buckets which places the point of interest furthest from either of its edges, and look in that bucket.
That same approach applies to GeoHashes. Take another look at the map of the world above. You’ll notice it’s superimposed over a grid which is recursively cut into quadrants. Each of those quadrants is simply one bit of latitude and one bit of longitude. So you’re first bit of latitude indicates whether you’re in the northern or southern hemisphere while the first bit of longitude places you in the eastern or western hemisphere. Remember, like I said earlier, 32 bits of latitude and 32 bits of longitude divides the world up into lots of one by one centimeter squares (actually they get to be quite narrow trapezoids as you approach the poles, but lets ignore that for now). If you want to check if two points happen to be in the square mile of earth, one quick way to check is to see if their latitudes and longitudes both start with the same X number of bits (where X is the appropriate number of bits to give you resolution at about the square mile level).
Back to the edge problem – suppose you have a point that is on an extreme edge! Take Greenwich, England for example. Suppose you’re happily sitting in a pub on the western hemisphere sharing a pint with one of your mates across the table from you – in the EASTERN hemisphere! You can’t get too much closer than sharing a drink at the same table, but from the perspective of our bucketing system, you’d each be treated as sitting on opposite ends of the Earth! What are we to do?
Adding a Third
Just add a third. Yep, you heard me right. Just add a third. Transform your complete coordinate system by adding a third to each the latitude and longitude. And in this case when I say a third, I mean 001010101010101010101.... I should probably take a step back here. Yes, we’re using 32 bit fixed point “integers” to represent our latitude and longitude, but for a moment, stop thinking of them as INTEGERS. I’m not talking about counting numbers here, I’m talking about fixed point binary numbers where the “decimal” (for lack of a better word) point comes before all the binary digits. So pretend 0001 actually refers to 0.0001 in binary. That means those binary Integers actually refer to fractions which range from 0 to just short of 1, of if you prefer to think of them as signed numbers, from negative one half to just shy of positive one half.
Adding one third – or adding one to every other bit – simply guarantees that any number which is locally near an edge won’t be near that same edge after the transformation takes place. That doesn’t mean they won’t be near some other edge, but for any given search you’re really only concerned about a local edge. So if you’re looking for people in the same square mile, you want to go with a transformation which keeps the center of the search away from edges of square mile buckets – not necessarily square half mile buckets. I’ll try to draw a better illustration of this next time, but I didn’t actually think I’d get this far in the explanation today…
Obviously with two dimensions you have two edges to deal with, so you potentially need to deal with four separate coordinate systems – except that really you don’t. Rather than adding a third, you could always subtract a third. Again, a picture would be worth a thousand words here, but suppose you have a point which is near the edge of a local bucket in terms of latitude, but not longitude, and it just so happens to be positioned such that when you add a third to both lat and long, you end up with it sitting near the longitudinal edge of it’s new bucket. Well, if you go back to the original number system and simply subtract a third rather than adding it, you’re guaranteed that neither latitude or longitude will be near an edge in the third space. So really you just need three spaces – the original and two transformations.
Ok, that’s it for today. Have fun in bizaro world =)